一、优限法
有特殊元素或特殊位置的排列问题，通常是先安排特殊元素或特殊位置，即优先处理特殊元素(或位置)法，简称优限法。
【例1】学校准备从5名同学中安排3人分别担任亚运会3个不同项目比赛的志愿者，其中张某不能担任射击比赛的志愿者，则不同的安排方法共有( )。
A.60种
B.24种
C.48种
D.36种
答案：C
【解析】共有三个项目，射击项目比赛对志愿者有限制要求，其他两类比赛没有，元素有限制要求用优限法。故优先选择射击运动志愿者，共有除小张4种选择，其他两个项目无要求有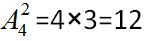
种选择，故不同的安排方法有4×12=48种。故选C。
二、捆绑法
解决元素相邻问题。元素要求相邻时，把相邻元素捆绑起来视为一个整体，再与其他元素进行排列，注意相邻的元素之间是否有顺序要求。
【例2】现在有五名男生和三名女生站成一排。若三名女生必须站在一起，则共有多少种不同的站法？
A.3440
B.3820
C.4410
D.4320
答案：D
【解析】这个题目当中我们看到题目要求三名女生必须站在一起，那其实就是说三名女生必须相邻。看到元素要求相邻的话呢，我们就要马上想到要去用捆绑法。因此我们在做题的时候直接把这三个女生绑在一起，把她们看成一个整体。
再与五个男生去进行任意排列，方法数有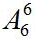
种。其次看内部需不需要顺序。女生的不同的站位会影响到最终的结果，所以说是需要顺序的，共有
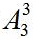方法。所以这道题一共有
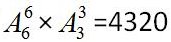种。选D。
三、插空法
解决元素不相邻问题。有元素要求不相邻时，先处理除不相邻元素以外的部分，再找出能够插入的空位，将不相邻的元素插入到不同的空位中。
【例3】某学习平台的学习内容由观看视频、阅读文章、收藏分享、论坛交流、考试答题五个部分组成。某学员要先后学完这五个部分，若观看视频和阅读文章不能连续进行，则该学员学习顺序的选择有( )种。
A.24
B.72
C.96
D.120
答案：B
【解析】根据题目中“观看视频和阅读文章不能连续”可知，此题可用插空法。
第一步，先排列除观看视频和阅读文章之外的三个元素，有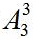种方法。
第二步，三个元素排列后可产生4个“空”，将“观看视频和阅读文章”插入其中两个“空”，有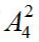
种，分步相乘，共有
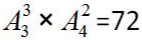种，故本题选B。
更多四川公务员行测技巧与方法扫码获取
